Count Derangements
In combinatorics, a derangement of a set is a permutation of its elements in which none of the elements appear in their original position. In other words, a derangement is a permutation such that no element is in its original position. That is the position you first found the elements.
I am simply saying, derangement is a situation where certain ordered things don't completely fall into their place of order (usual arrangement)
The number of derangements of a set of n distinct elements is called the "subfactorial" of n and is denoted by !n and is read as "n subfactorial" or "n derangements".
Such situations include:
- You shuffle a deck of cards labeled 1-9. If none of their cards occupy their usual position after the shuffle, then it is a derangement.
- A secretary with letters labeled with their respective owners as well as envelopes also labeled with their owners. If after placing all the letters in the envelopes & none match their owners, then that is a derangement.
- You go to a graduation ceremony & throw your hats. If finally, everybody goes home with a hat that was not originally theirs then that is a derangement.
For example:
The derangements of {1, 2} are {2, 1}.
The derangements of {1, 2, 3} include {2, 3, 1} and {3, 1, 2}.
The derangements of {1, 2, 3, 4} include {2, 1, 4, 3}, {3, 4, 1, 2}, and others.
The formula for the sub-factorial of n, denoted as !n, is often defined recursively:
!n=(n−1)⋅(!(n−1)+!(n−2))!n=(n−1)⋅(!(n−1)+!(n−2))
with base cases !0=1!0=1 and !1=0!1=0.
Calculating derangements can be a non-trivial task, and various methods, including recursive formulas and inclusion-exclusion principles, are used to compute them efficiently. The concept of derangements has applications in various areas of mathematics and computer science, including probability theory and algorithm analysis.
Note: Derangements are permutations with no fixed points.
Recurrence Relation: Graduation
Here, I want to try and derive the recurrence relation for a case of students throwing their hats during a graduation ceremony.
Base Case
The first scenario is a case where we have only one student. In such a case the number of derangements is 0 represented as follows.
CountDerangements(1) = 0
The second scenario is a case where you have two students who can only exchange their hats. Here, there can only be one derangement.
i.e.
CountDerangements(2) = 1
Using the two cases, I want to generalize for a case of 4 students and generate a general case from it.
CountDerangements(4) = 4-1 * (CountDerangements(3) + CountDerangements(2))
= 4-1 * (CountDerangements(3) + 1)
Let's pose there as I take this time to evaluate the CountDeragements(3).
CountDerangements(3) = 3-1(CountDerangements(2) + CountDerangements(1) )
=2(1 + 0)
=2
Now, I will proceed by providing the CountDerangements(3) as follows:
= 4-1 * (CountDerangements(3) + 1)
= 3 * (2 + 1)
=3*3
=9
This example clearly illustrates the concept of optimal substructure.
The optimal substructure is when you have to build your solution as part of smaller blocks of your problem.
And that is the case we have above. Essentially, to find the solution of n, we first need to find the solution to smaller instances of the same problem i.e. n-1, and n-2. Below is the representation of this generic case.
CountDerangements(n) = 0 if n==1
1 if n==2
(n-1)(CountDerangements(n-1) + CountDerangements(n-2))
Solution: Count Derangements Recursive
class CountDerangementsRec:
def __init__(self, set_size):
self.set_size = set_size
def count_derangements(self):
return self.count_derangements_rec(self.set_size)
def count_derangements_rec(self, n):
if n == 1:
return 0
if n == 2:
return 1
return (n-1) * (self.count_derangements_rec(n-1) + self.count_derangements_rec(n-2))
for i in range(1, 11):
n = CountDerangementsRec(i).count_derangements()
print("Recursive derangements in set size {} -> {}".format(i, n))
Time Complexity
The time complexity of the provided recursive solution is exponential, specifically O(2^n). This is because, for each call to count_derangements_rec(n), it makes two recursive calls: one with n−1 and another with n−2. The number of recursive calls grows exponentially with the input size, resulting in an exponential time complexity.
Now that we are here, I actually this function is a super exponential function and will overtake the exponential function.
Let's consider the following few examples:
1 2 3 4 5 6 7 8 9
0 1 2 9 44 265 1854 14833 133496
If you consider these examples, you realize that this function(!n) grows so fast that it is bigger than exponential.
Space Complexity
The space complexity is determined by the maximum depth of the recursion, which is n in this case. Therefore, the space complexity is O(n). Each recursive call consumes space on the call stack, and since there can be at most n recursive calls active at the same time, the space complexity is linear.
Solution: Count Derangements Top-Down
I will use the following diagram to best illustrate the case of overlapping subproblems for a case where n is 6.
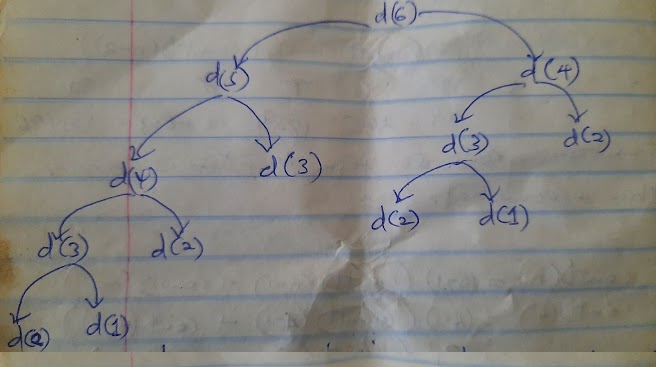
In Memoization(top-down), when we store a value, it never times out(we never remove the solution from our temporary space), unlike caching which implies that the values might be removed.
In top-down, we start working our solution tree from the top for every new sub-solution that we have. We store it in our array and then if we require the same answer to the same sub-solutions we read it from the array.
class CountDerangementsTopDown:
def __init__(self, set_size):
self.set_size = set_size
self.dp ={}
self.dp[1] =0
self.dp[2] =1
def count_derangements(self):
return self.count_derangements_rec(self.set_size)
def count_derangements_rec(self, n):
if n in self.dp:
return self.dp[n]
else:
results= (n-1) * (self.count_derangements_rec(n-1) + self.count_derangements_rec(n-2))
self.dp[n] = results
return self.dp[n]
for i in range(1, 66):
n = CountDerangementsTopDown(i).count_derangements()
print(" Top Down Derangements in set size {} -> {}".format(i, n))
The time & space complexity of the memoization solution is both O(n).
Solution: Bottom-up Dynamic Programming
The Bottom-up solution usually has the same performance as the top-down solution, but it kind of simplifies your solution and lets you see if there are other areas to improve your solution.
The idea of the bottom-up solution is to compute the temporary space from the start to our global solution. We will still need this temporary and +1 space for the bottom-up solution.
class CountDerangementsBottomUp:
def __init__(self, set_size):
self.set_size = set_size
self.dp ={}
self.dp[1] =0
self.dp[2] =1
for i in range(3, self.set_size+1):
if i in self.dp:
return self.dp[i]
self.dp[i] = (i-1) * (self.dp[i-1] + self.dp[i-2])
def count_derangements(self):
return self.dp[self.set_size]
for i in range(1, 100):
n = CountDerangementsBottomUp(i).count_derangements()
print(" Bottom up Derangements in set size {} -> {}".format(i, n))
Time Complexity
Let n be the set size. The loop runs for n iterations, and within each iteration, the computation involves basic arithmetic operations. Therefore, the overall time complexity of the bottom-up dynamic programming approach is O(n).
Space Complexity
The space complexity is determined by the size of the dynamic programming table (self.dp). In this case, the table stores the derangements for each set size up to n. Therefore, the space complexity is O(n) as well.
By using the bottom-up solution, we explore it to find areas of optimization in the case of memory utilization as follows:
Solution: Optimized Bottom-Up Dynamic Programming Solution
class CountDerangementsBottomUpOpt:
def __init__(self, set_size):
self.set_size = set_size
self.first =0
self.second =1
for i in range(3, self.set_size+1):
temp = (i-1) * (self.first + self.second)
self.first=self.second
self.second = temp
def count_derangements(self):
return self.second
for i in range(1, 100):
n = CountDerangementsBottomUpOpt(i).count_derangements()
print("Optimized Bottom up in set size {} -> {}".format(i, n))
In the optimized solution above, the time complexity remains O(n). However, the space complexity is reduced to O(1).

Join the Discussion
No comments yet. Be the first to share your thoughts!